Fermaova poslednja teorema: 10 tajni velike matematičke misterije
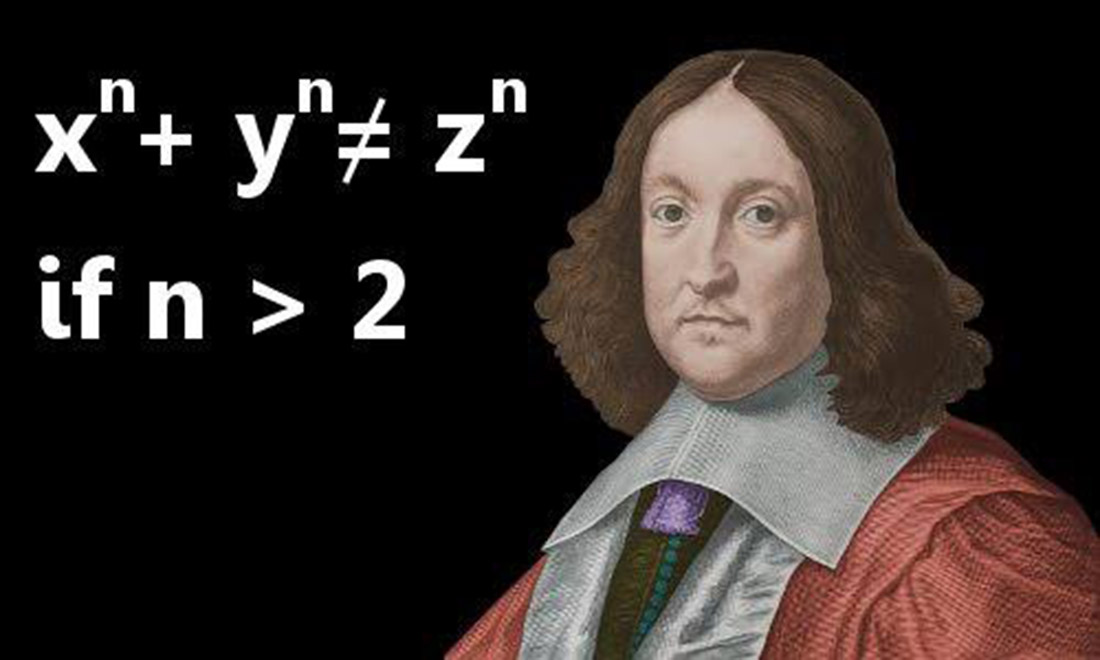
Fermaova poslednja teorema, koji je postavio francuski matematičar Pjer de Ferma u 17. veku, predstavljao je jedan od najpoznatijih matematičkih problema u istoriji. Iako se na prvi pogled čini jednostavnim, ova teorema je izazvala glavobolje matematičarima više od 350 godina.
Na marginama svoje knjige “Arithmetica”, Ferma je zapisao da poseduje “čudesan dokaz” koji podkrepljuje teoremu, ali ga nikada nije otkrio. Tek krajem 20. veka, britanski matematičar Endrju Vajls konačno je uspeo da dokaže ovau teoremu, stavljajući tačku na jedan od najdužih nerazrešenih problema u matematici i otvarajući nove puteve za buduća istraživanja.
10. Ferma nije otkrio dokaz za svoju teoremu
Da li znate… da je Pjer de Ferma, jedan od najpoznatijih matematičara iz 17. veka, zapisao na margini knjige “Arithmetica” tvrdnju koja će kasnije postati poznata kao Fermaova poslednja teorema?
U toj belešci, Ferma je napisao da ima “čudesan dokaz” koji je predugačak da bi stao u marginu. Iako je ovaj komentar izazvao interesovanje mnogih matematičara kroz vekove, Ferma nikada nije otkrio taj dokaz.
Mnogi stručnjaci veruju da je Ferma možda imao ideju za dokaz, ali da ona nije bila kompletna ili tačna. Umesto toga, njegova beleška podstakla je brojne matematičare da se upuste u viševekovnu potragu za dokazom, što je dovelo do razvoja novih teorija i metoda u matematici. Taj misterijski “čudesan dokaz” ostao je jedna od najvećih zagonetki u istoriji matematike sve do kraja 20. veka.
09. Više od 350 godina bez rešenja
Da li znate… da je Fermaova poslednja teorema ostala nerešena više od 350 godina, iako je izazvao ogromno interesovanje i napore mnogih velikih matematičara?
Teorema, koja tvrdi da ne postoje tri pozitivna cela broja aaa, bbb i ccc koja zadovoljavaju jednakost an+bn=cn za n>2, bio je izuzetno teško dokazati.
Iako je bilo nekoliko pokušaja da se teorem dokaže, svaki je završavao neuspehom. Tek 1994. godine, engleski matematičar Endrju Vajls, posle višegodišnjeg rada u tajnosti, uspeo je da dokaže teoremu koristeći metode iz modernih grana matematike, uključujući teoriju modularnih formi i algebarsku geometriju. Vajlsov uspeh nije bio samo dokazivanje jedne teoreme, već je označio prekretnicu u matematici, rešavajući problem koji je bio izazov generacijama matematičara.

08. Problem je inspirisao razvoj novih grana matematike
Da li znate… da je pokušaj rešavanja Fermaova poslednja teorema značajno uticao na razvoj novih grana matematike?
Tokom vekova, dok su matematičari pokušavali da pronađu dokaz za teoremu, razvijene su nove teorije i metode koje su transformisale matematiku.
Na primer, pokušaji rešavanja ovog problema doveli su do razvoja algebarske geometrije, koja je postala jedna od najvažnijih oblasti u savremenoj matematici. Takođe, istraživanja u teoriji brojeva, koja proučava osobine brojeva i njihove odnose, značajno su napredovala zahvaljujući naporima da se dokaže Fermaova teorema.
Ova teorema je, na neki način, postala katalizator za matematičke inovacije i istraživanja, podstičući matematičare da istraže nove puteve i metode koji su na kraju doveli do njegovog dokaza.
07. Teorema kao “najpoznatiji nerazrešeni problem”
Da li znate… da je Fermaova poslednja teorema decenijama bila poznata kao “najpoznatiji nerazrešeni problem” u matematici?
Još od trenutka kada je Pjer de Ferma zapisao svoj čuveni komentar na margini knjige, teorema je postala izazov za generacije matematičara. Bez obzira na svoju jednostavnu formu, teorema je odolevao svim pokušajima da bude dokazana.
Tokom 18. i 19. veka, mnogi istaknuti matematičari, uključujući Eulera, Legandra i Dirihlija, posvetili su svoje napore pokušajima da dokažu teoremu za specifične vrednosti n. Međutim, opšti slučaj za sve vrednosti n>2 ostao je nerešen. Ova teorema je postala sinonim za matematičku misteriju, a njegovo rešavanje smatrano je Svetim gralom matematike. Tek krajem 20. veka, više od tri veka nakon što je postavljena, Fermaova poslednja teorema konačno je dobiola svoj dokaz, stavljajući tačku na jednu od najdužih potraga u istoriji nauke.
06. Vajlsov dokaz je zahtevao korišćenje savremene tehnologije
Da li znate… da je Endrju Vajls, dok je radio na dokazu Fermaove poslednje teoreme, morao da koristi savremenu tehnologiju kako bi proverio i potvrdio tačnost nekih delova svojih proračuna?
Iako je većina Vajlsovog rada zasnovana na klasičnim matematičkim tehnikama i njegovom dubokom znanju teorije brojeva, kompleksnost problema zahtevala je dodatnu proveru kroz upotrebu računarskih programa.
Vajls je proveo gotovo deceniju radeći u tajnosti na problemu, svesno izbegavajući pažnju matematičke zajednice kako bi mogao neometano da se posveti zadatku. Korišćenje računara bilo je ključno u njegovom radu, jer je omogućilo analizu složenih struktura i proveru velikih količina podataka koji bi ručno bili skoro nemogući za obradu. Ova kombinacija tradicionalnih matematičkih metoda i moderne tehnologije bila je presudna za Vajlsov uspeh u rešavanju teorema.
05. Dokaz je sadržao grešku
Da li znate… da je prvobitni dokaz Endrjua Vajlsa, koji je predstavio 1993. godine, sadržao grešku koja je mogla da poništi čitav rad?
Nakon što je Vajls objavio svoj dokaz, matematička zajednica bila je ushićena, ali su ubrzo otkrili da postoji ozbiljan problem u jednom delu dokaza.
Vajls i njegov saradnik, Ričard Tejlor, uložili su ogroman napor u ispravljanje ove greške. Tokom cele godine, Vajls je neumorno radio na pronalaženju rešenja. Konačno, 1994. godine, Vajls je uspeo da pronađe ispravku za grešku, što je omogućilo da dokaz bude prihvaćen kao ispravan. Ovaj trenutak bio je prekretnica u istoriji matematike i označio je kraj jedne od najdužih i najintenzivnijih potraga za matematičkim dokazom.
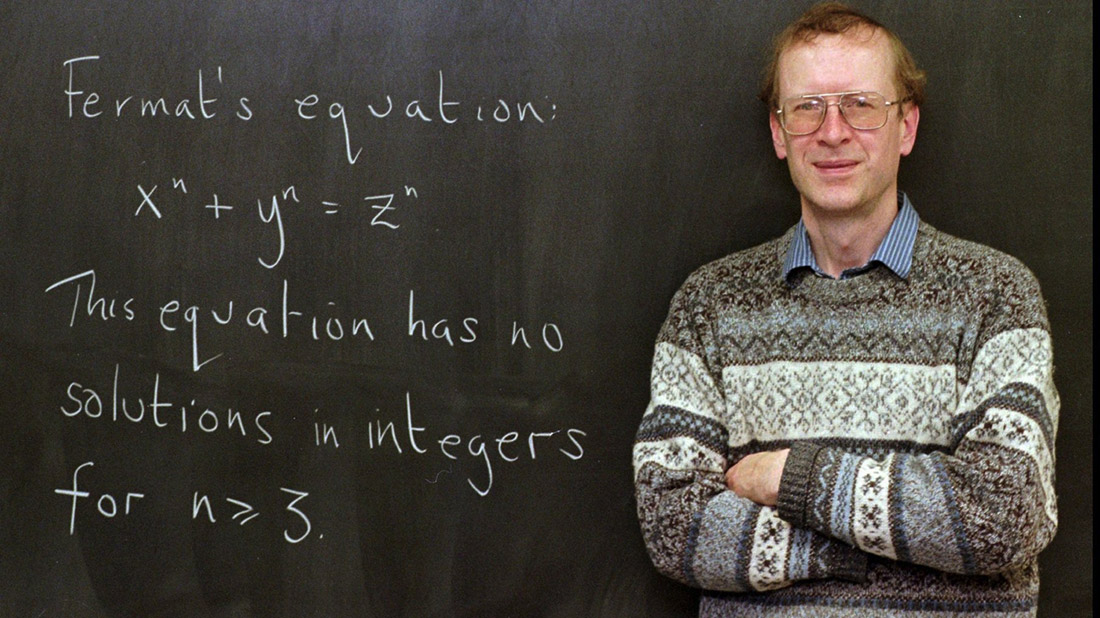
04. Inspiracija za popularnu kulturu
Da li znate… da je Fermaova poslednja teorema postala inspiracija za mnoga dela popularne kulture, uključujući knjige, filmove, pa čak i televizijske serije?
Ova teorema, zbog svoje misterioznosti i dugotrajne nerešenosti, privukla je pažnju ne samo matematičara, već i šire javnosti, umetnika i pisaca.
Jedan od najpoznatijih primera je roman “Teorema o papiru” (eng. “The Oxford Murders”) španskog pisca Giljerma Martineza, koji prati priču o matematičaru i njegovom studentu dok pokušavaju da reše niz zagonetnih ubistava povezanih sa matematičkim teoremima, uključujući i Fermaova poslednja teorema. Ova teorema se takođe pojavljuje u filmu “Pi: The Mathematician’s Enigma” (1998), gde je deo šire narativne teme o matematičkim misterijama i opsesijama.
Pored toga, popularne TV serije kao što su “Simpsonovi” i “Teorija velikog praska” povremeno spominju ovu teoremu, često kao deo šala koje se tiču matematike i nauke. Fermaova poslednja teorema postala je deo pop kulture, što je dodatno povećalo njegovu prepoznatljivost i van matematičkih krugova.
03. Matematički klubovi i izazovi
Da li znate… da su Fermaova poslednja teorema i pokušaji njegovog rešavanja postali osnova za mnoge matematičke klubove, izazove i takmičenja širom sveta?
U matematičkim zajednicama, teorema je često korišćen kao simbol krajnjeg izazova, privlačeći najtalentovanije matematičare i entuzijaste.
Na univerzitetima i u matematičkim klubovima, studenti i profesori okupljali su se kako bi diskutovali o različitim aspektima teoreme i predložili moguće metode za njegovo rešavanje. Ovi događaji su često bili prateći momenti na matematičkim konferencijama ili kao deo specijalnih seminara posvećenih teoriji brojeva.
Takođe, popularnost Fermaove poslednje teoreme nije bila ograničena samo na akademsku zajednicu. Organizovana su i javna predavanja i radionice, gde su se matematičari obraćali široj publici, objašnjavajući zašto je ova teorema toliko značajan i kako je njegova nerešenost inspirisala generacije naučnika. Čak i nakon što je teorema konačno dokazana, ostao je simbol matematičkog izazova, podstičući nove generacije matematičara da istražuju složene probleme i tragaju za rešenjima.
02. Teorem je vezan za teoriju modularnih formi
Da li znate… da je ključ za rešavanje Fermaovog poslednjeg teorema ležao u teoriji modularnih formi, specifičnih za Taniyama-Šimurinom teoremu?
Ova teorija, koja se bavi proučavanjem složenih matematičkih struktura i njihovih odnosa, pokazala se ključnom za dokazivanje teoreme koja je odolevala vekovima.
Taniyama-Šimurina hipoteza, koja je predložena sredinom 20. veka, postavila je most između dve naizgled nepovezane oblasti matematike: teorije eliptičnih krivih i teorije modularnih formi. Endrju Vajls je, koristeći ovu hipotezu, uspeo da napravi presudan korak u rešavanju Fermaove poslednje teoreme.
Ovaj neočekivani spoj različitih matematičkih grana bio je ključ za Vajlsov uspeh. Pokazalo se da su eliptične krive koje zadovoljavaju određene uslove povezane sa modularnim formama, što je omogućilo da se teorema dokaže. Vajlsov dokaz ne samo da je rešio jedan od najstarijih problema u matematici, već je i potvrdio jednu od najvažnijih hipoteza u modernoj matematici, čime je obogatio naše razumevanje ovih kompleksnih matematičkih struktura.
01. Nobelova nagrada nije dodeljena
Da li znate… da za matematička dostignuća ne postoji Nobelova nagrada, što znači da Endrju Vajls nije mogao da dobije ovo najprestižnije priznanje za svoj rad na Fermaovoj poslednjoj teoremi?
Nobelove nagrade dodeljuju se za izuzetna dostignuća u oblastima poput fizike, hemije, medicine, književnosti i mira, ali matematika nije među njima.
Ipak, Vajlsovo dostignuće nije ostalo nezapaženo. Za svoj rad na rešavanju Fermaove poslednje teoreme, Vajls je dobio brojne druge prestižne nagrade. Među njima su Abelova nagrada, koja se često naziva “Nobelovom nagradom za matematiku”, i Fildsovu medalju, koja je jedno od najviših priznanja u matematici, iako se obično dodeljuje matematičarima mlađim od 40 godina.
Vajlsovo dostignuće smatralo se toliko značajnim da mu je, osim Abelove nagrade, dodeljena i posebna čast u vidu člana Kraljevskog društva, kao i priznanje za životno delo od strane Matematičkog društva Londona. Njegov rad na Fermaovoj poslednjoj teoremi ostaje jedno od najvažnijih dostignuća u istoriji matematike.
Fermaovog poslednjeg teorema, nakon više od tri veka izazova i misterije, ostaje jedno od najfascinantnijih dostignuća u istoriji matematike. Njegova rešivost nije samo dokaz matematičkog genija, već i primer kako upornost, inovacija i interdisciplinarni pristup mogu dovesti do revolucionarnih otkrića. Dokaz Endrjua Vajlsa ne samo da je razrešio problem koji je mučio matematičare vekovima, već je otvorio vrata novim oblastima istraživanja i inspirisao buduće generacije matematičara. Fermaov poslednji teorem ostaje simbol matematičke istrajnosti i duboke povezanosti između različitih grana matematike.


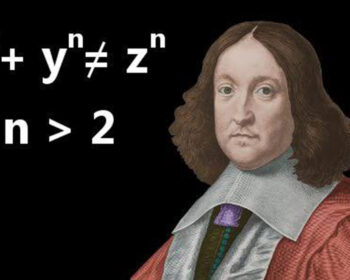
Odgovori